算法日记 - 数组五连

OS: 不知道先放代码还是先放图解，就随性一点吧，随机出现先放代码、先放图片....（雾）

LC704 二分查找

704. 二分查找 - 力扣（LeetCode）

  // 这个写法摘自邓公，邓俊辉老师，感谢老师的循循善诱.  
  int search(vector<int>& nums, int target) {
        // 通过 (low + hi)/2 确定中轴mid
        // target 和中轴mid比较 这时会出现三种情况.
        // case a - target < mid : 目标元素可能在中轴左边，移动右边界hi到中轴前一个的位置(因为中轴比较过了，所以可以直接跳到中轴前一个)
        // case b - target > mid : 目标元素可能在中轴右边，移动左边界到中轴的右边前一个位置套路同上
        // case c - target == mid ： 返回mid,mid 就是目标元素在数组中的下表 
        int lo = 0, hi = nums.size() - 1, mid = -1;
        // 在上面的过程中lo,hi边界总会重叠在一起(无线二分下去，会逐渐缩小)，所以lo <= hi
        while(lo <= hi)
        {
            mid = (lo + hi) >> 1;
            if(target > nums[mid]) lo = mid + 1;
            else if(target < nums[mid]) hi = mid - 1;
            else if(target == nums[mid]) return mid;
        }
        return -1;
    }

LC27 移除元素

27. 移除元素 - 力扣（LeetCode）

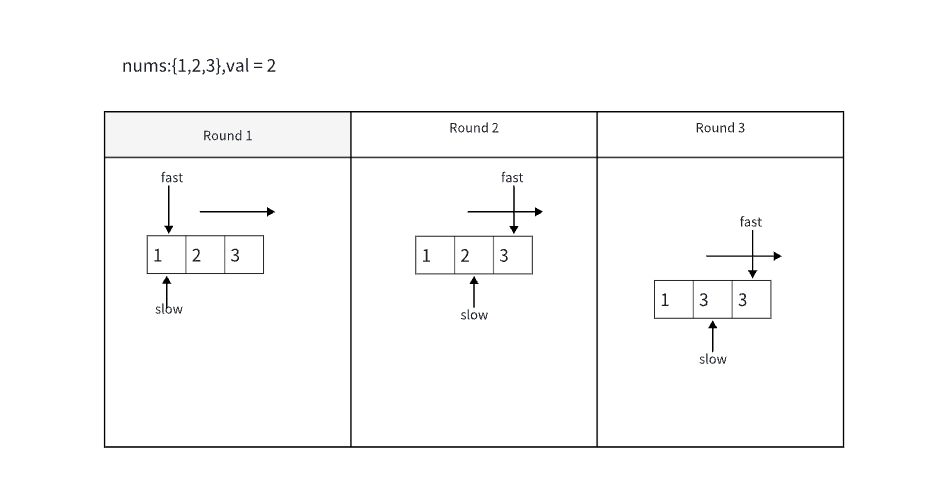
    int removeElement(vector<int>& nums, int val) {
        // 这个相当于快慢指针的变种吧或者双指针?(雾) [双指针原先时重叠的，遇到目标元素快指针跳过，慢指针不动...]
        int slowIndex = 0, fastIndex = 0;
        while(fastIndex < nums.size()){
            if (nums[fastIndex] != val) nums[slowIndex ++] = nums[fastIndex ++];
            else fastIndex ++;
        }
        // 返回值优点脑筋急转弯，快指针跳过了几个遍历到最后快指针停止，两指针之间的元素差就是找到了几个目标元素。而slowindex停的位置刚好就是移除后剩下元素的数组长度。推导见下:
       // 假设 原数组有元素M个，移除元素N个，那么就有
       // M - N = slowIndex
       // 因为 fastIndex = M - 1,所以有 slowIndex = fastIndex + 1 - N;
       
        return slowIndex;
    }

LC977 有序数组平方和

977. 有序数组的平方 - 力扣（LeetCode）

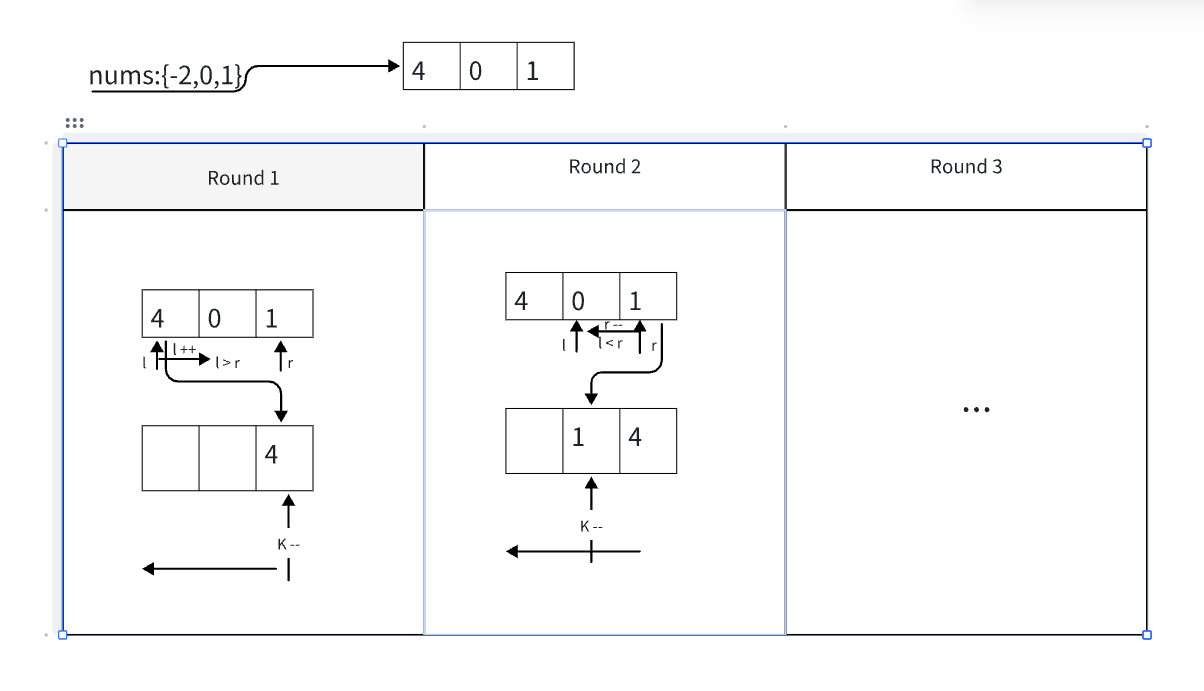
    vector<int> sortedSquares(vector<int>& nums) {
        int l = 0, r = nums.size() - 1, k = r,retL,retR;
        vector<int> vret(k+1,0);
        while(l<=r){
            retL = nums[l]*nums[l];
            retR = nums[r]*nums[r];
            if (retL < retR)
            {
                vret[k--] = retR;
                --r;
            }else{
                vret[k--] = retL;
                ++l;
            }
        }
        return vret;
    }

LC209 长度最小的子数组

209. 长度最小的子数组 - 力扣（LeetCode）

给定一个数组nums 和目标值target

限制条件:

• 1 <= nums.length <= 10^5

题目要求

• 如果数组里有连续子序列累加和 >= target, 找出这些连续子序列，并最终返回满足条件的最短连续子序列长度

• 不满足，返回 0

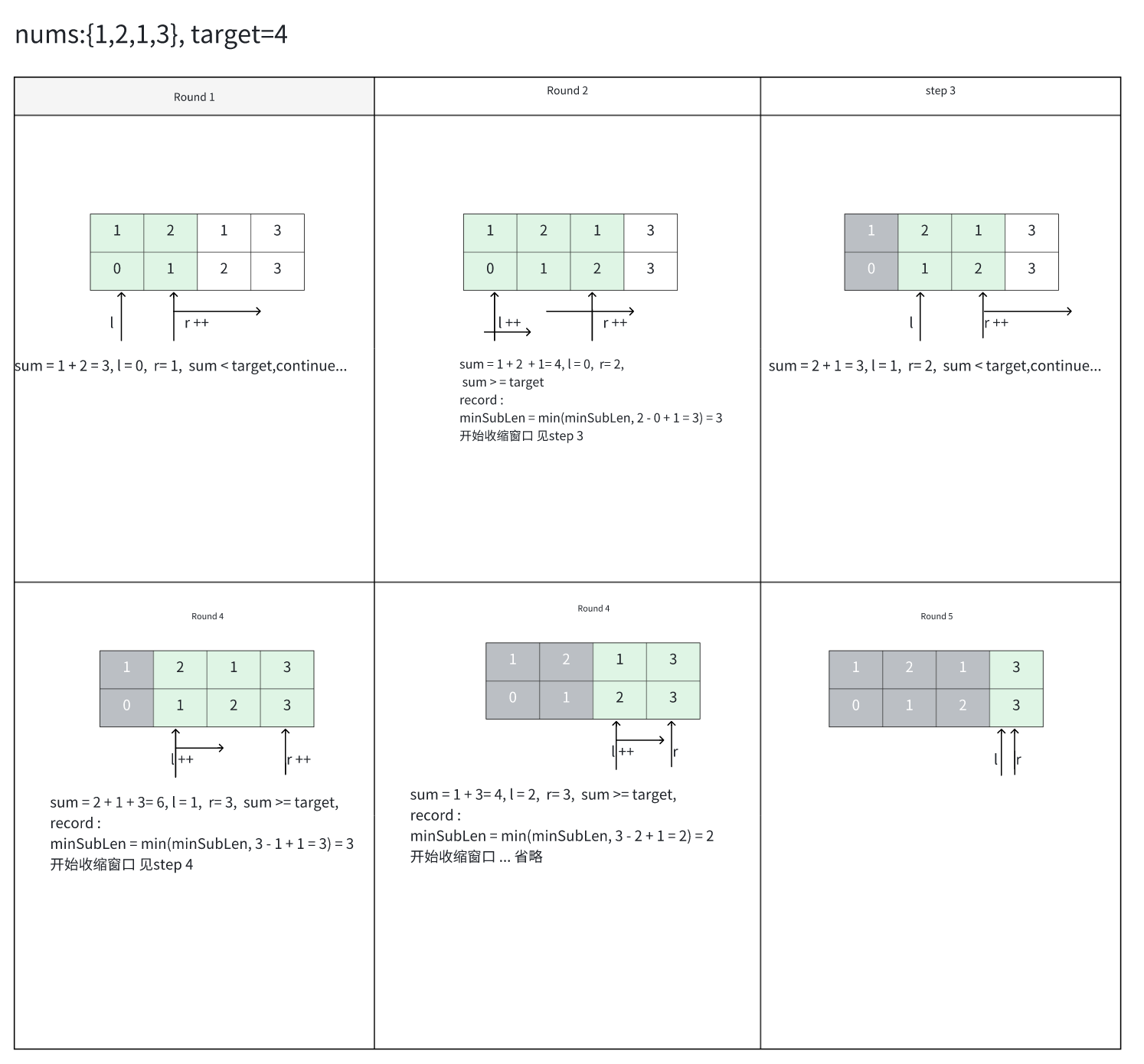
    int minSubArrayLen(int target, vector<int>& nums) {
        int MinSubLen = INT32_MAX/* 这里用比题目给出最大数组个数的数也可以，这么写只是更规范(可读性？) */,l = 0, sum = 0;
        // 双指针，l 窗口左边界以数组0初始，r 窗口右边界
        // 1 累计和sum 随着r右移(窗口扩大)，不断累加
        // 2 直到累加到满足条件 累加和 >= target (sum >= target)
        // 3 求出右边界元素到左边界元素的距离 + 1 --> 就是窗口中的元素个数 (r - l + 1) -> 更新最小长度记录
        // 4 收缩窗口 左边界 l 往右移 重复 同时sum 吐出左边界收缩踢出的元素x sum -= x
        // 5 判断是否满足 sum >= target，满足 跳3 继续流程，不满足跳1 继续流程 
        for(int r = 0; r < nums.size(); ++ r)
        {
            sum += nums[r];
            while(sum >= target)
            {
                MinSubLen = min(MinSubLen,(r - l + 1));
                sum -= nums[l++]; 
            }
        }
        // 这里 == 的原因是 当不等于是说明这个有更新过(MinSubLen 被改过，所有存在至少一个序列，所以不反回0，否则返回0)
        return (MinSubLen == INT32_MAX ? 0 : MinSubLen); 
    }

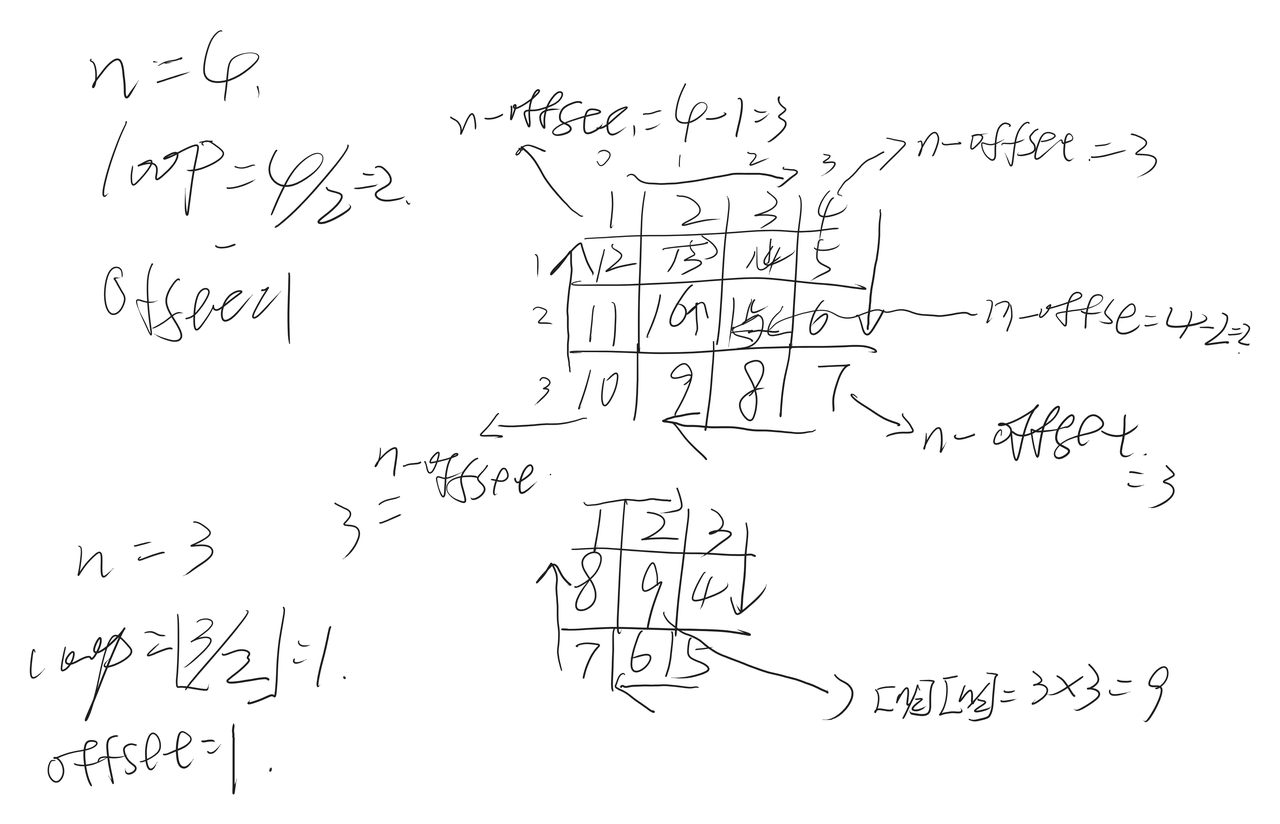
LC59 螺旋矩阵II

59. 螺旋矩阵 II - 力扣（LeetCode）

class Solution {
public:
    vector<vector<int>> generateMatrix(int n) {
        vector<vector<int>> Matrix(n,vector<int>(n,n));
        if (n == 1) return Matrix;
        int loop = n / 2, counter = 1, offset = 1, startX = 0, startY = 0, i, j;
        while(loop --)
        {
            // 其实可以把i,j初始化放这里，统一初始化 i = startX, j = startY;
            i = startX, j = startY;
            // toplet -> topright 
            for (; j < n - offset; ++ j) // 初始化本轮 j : for(j = startY; j < n - offset; ++ j)
                Matrix[startX][j] = counter ++; // 这里不能写[i][j]
            // topright -> rightbottom // 从这里开始就不能用 [startX][j]/[i][startY] 去左做角标变量 因为上面i 已经被改过
                                       // 这一行又开始改变 j 所以从这行开始后边都是用[i][j] 去做角标变量（因为i,j 都被改了）
            for (; i < n - offset; ++ i) // 初始化本轮 j: for (i = startX; i < n - offset; ++ i)
                Matrix[i][j] = counter ++; // 列迭代计数器位置已经到了末尾，列角标不能用startY,这等于回到最前一列，所以不能用[i][startY] 而是[i][j]
            // rightbottom -> leftbottom
            for (; j > startY; -- j)
                Matrix[i][j] = counter ++ ;
            // leftbottom -> topleft
            for (; i > startX; --i)
                Matrix[i][j] = counter ++;
            startX ++; startY ++; offset ++;
        }
        if (n & 1) Matrix[n/2][n/2] = counter;
        return Matrix;
    }
};